【数据结构】学习计划

古人言：“王道领进门，修仙在个人。”做题训练，是考研修仙的必经之路，预祝大家在每一个环节，都能修真悟道，成功渡劫。

根据题目难度不同，修仙等级有三：

• 掌握第一等级题目的同学，江湖人称——“道上人”；
• 掌握第二等级题目的同学，江湖人称——“道上佬”；
• 掌握第三等级题目的同学，江湖人称——“道上仙”。

愿各位潜心修炼，我们顶峰相见。

Week 1 学习计划总览

Week 1 学习计划总览

Day 1 学习计划

今天推荐的学习内容为1.1、1.2两个小节。

其中，1.1小节涉及的知识点会在后续章节中还会有更深入的学习，第一次学习对概念有模糊感很正常，莫慌~

本节内容的重难点是要注意区分“逻辑结构”和“物理结构”。另外，小题 2、3、4、7 和 大题 1、2 涉及到后续章节的学习内容。通过以后的学习，大家的理解会越来越清晰哒~

1.2 小节为高频考点。408选择题常考察时间复杂度分析，一定要通过课后习题练习技巧，掌握出题套路。

1.1 数据结构的基本概念

学习建议

• 本节涉及的知识点会在后续章节中不断重复，第一次学习对概念有模糊感很正常，莫慌~
• 注意区分“逻辑结构”和“物理结构”。

考研修仙

• 道上人：掌握数据结构的基本概念。

  • 小题 1、5、6

  小题 5

• 道上佬：区分常见数据结构的逻辑、物理特性

  • 小题 2-4、7

  这些题目涉及后续章节的知识，不会做也莫慌

  错题：小题 4

• 道上仙：深入理解数据结构三要素之间的关系

  • 大题 1
  • 大题 2

  通过后续章节的学习，更容易理解

1.2 算法和算法评价

学习建议

• 408选择题常考察时间复杂度分析，一定要通过课后习题动手练习

考研修仙

• 道上人：掌握什么是算法，理解时间、空间复杂度的意义

  • 小题 1、2、12

  错题：小题 12

• 道上佬：学会阅读程序，分析复杂度（循环、递归）

  • 小题 3、9-11
  • 大题 1
  • 大题 2

• 道上仙：体会真题考法

  • 小题 4-7

  错题：小题 6

Day 2~3 学习计划

接下来推荐的学习内容为2.1、2.2两个小节。

其中，2.1 节从数据结构三要素的两个方面，即“逻辑结构”、“数据的运算”对线性表进行定义，而数据结构的具体实现还需要考虑“物理结构”的问题。后续两个小节会分别探讨线性表的“顺序存储实现”和“链式存储实现”。

2.2 节为考研算法题的命题重点，要求大家能够熟练手写顺序表相关代码。在历年真题中，常结合“查找”和“排序”两个章节的内容考察。因此第一轮复习时，做不出课后真题很正常。

本节课后习题的大题部分，涉及手写代码，因此可能做题要花不少时间，第一次复习千万不能慌，打好基础，稳住，才能赢~

2.1线性表的定义和基本操作

学习建议

本节从数据结构三要素的两个方面，即“逻辑结构”、“数据的运算”对线性表进行定义，而数据结构的具体实现还需要考虑"物理结构"的问题。后续两个小节会分别探讨线性表的"顺序存储实现"和"链式存储实现"。

考研修仙

• 道上人：掌握线性表的逻辑特性

  • 小题 1-3

• 道上佬：NULL

• 道上仙：NULL

2.2 线性表的顺序表示

学习建议

• 本节为考研算法题的命题重点，要求大家能够熟练手写顺序表相关代码。
• 在历年真题中，常结合”查找”和”排序”两个章节的内容考察。因此第一轮复习时，做不出课后真题很正常。
• 本节课后习题的大题部分，涉及手写代码，因此可能做题要花不少时间

考研修仙

• 道上人：理解顺序表的特点

  • 小题 1-3、11

  错题：小题 2

• 道上佬：熟练掌握顺序表基本操作的实现

  • 小题 4-10
  • 大题 1
  • 大题 2
  • 大题 3
  • 大题 4
  • 大题 5
  • 大题 6

  错题：大题 3、6

• 道上仙：顺序表的灵活应用

  • 大题 7
  • 大题 9

  错题：大题 9

Day 4~6 学习计划

推荐开始学习2.3线性表的链式表示。本节是考研算法题的命题重点，要求大家能够熟练手写链表相关代码。难度和题量相对较大，大家可以花3天左右时间完成哦！

2.3 线性表的链式表示

学习建议

本节也是考研算法题的命题重点，要求大家能够熟练手写链表相关代码。在历年真题中，算法题几乎是基于“顺序表”和“链表”，因此对于2.2、2.3小节的训练，可以让大家打牢算法题基础。

本节课后习题的大题部分，涉及手写代码，因此可能做题要花不少时间单链表的“头插法”和“逆置”思想很常考，注意从题目中体会。

考研修仙

• 道上人：理解单链表的特点

  • 小题 7， 9

  建议大家尝试手写实现单链表的基本操作，包括：用struct结构体定义单链表；头插法、尾插法建立单链表；单链表的插入、删除、按值查找、按位查找。

• 道上佬：熟练掌握单链表的操作（理论和代码）

  • 小题 3、6、8、10-14
  • 小题 16-19、22、25
  • 大题 1
  • 大题 2
  • 大题 3
  • 大题 4
  • 大题 5
  • 大题 6
  • 大题 7
  • 大题 10
  • 大题 11
  • 大题 12

  其中，大题6涉及排序，为第8章内容

  • 大题2：对比学习2.2.3 大题3
  • 大题4：对比学习2.2.3 大题1
  • 大题5：对比学习2.2.3 大题2
  • 大题7：对比学习2.2.3 大题5
  • 大题10、11：对比学习，11与5头插法对比
  • 大题12：对比学习2.2.3 大题6

  错题：小题 8、19

  错题：大题 1、3、4、5

• 道上仙：理解复杂链表，比较单链表与复杂链表的优劣（根据不同情况选最合适的链表），比较顺序表和链表的优劣

  • 小题 1、2、4、5、20、21、24
  • 大题 8
  • 大题 9
  • 大题 13
  • 大题 14
  • 大题 15
  • 大题 16
  • 大题 17
  • 大题 18
  • 大题 19
  • 大题 20

  其中：

  • 大题13：为头插法应用
  • 大题14、15：为顺序查找应用

  错题：小题 1、4、5、20、24

本周内容总结

过去这一周，我们学习了第一、第二章的内容。不知大家感受如何？第一章中，时间复杂度分析为每年必考，可能独立作为一个小题，也会结合算法题进行考察。当然，偶尔也有些年份会考察空间复杂度。

408试卷中，数据结构通常为两个大题，每年只有一个大题是算法题（需要手写代码）。而第二章是算法题的核心章节，从2009年教育部开始推出408计算机统考以来，13年中有9年的算法题都是考察顺序表或链表。通常来说，还要结合第七章（查找）、第八章（排序）的知识，才能处理这些算法题。因此目前这个阶段看见真题的算法题没思路很正常，不要慌。但是在第一轮复习中，时间还很充裕，大家应该多练习手写代码，通过我们为大家挑选的大题，打牢手写代码的基础，厚积薄发。

Tips：我们在选题时排除了近五年的真题，大家可以把这些题目先留下，后期冲刺阶段作为套题训练。另外，题目分三个等级难度，在第一轮复习时，如果你觉得某些大题做着很吃力，也不用着急，给自己一些时间，以后再回来做也是可以的（当然，能做还是尽量做吧~）

鉴于Week1的问卷反馈，大家普遍的问题是关于代码的实现，咸鱼老师给出以下Tips 👇👇👇

• 跨考生的话第一轮复习代码写不出来是正常的，可以以选择题和大题理解为主，很多代码考试时都不会考，不会写问题也不大
• 你对着书想一下什么代码15分钟能写完，就可能是出题点，超过15分钟基本不用考虑了（如先、中、后序遍历非递归），一般都是很常见的偏思考和技巧一点，而不是大段代码
• 着重复习数组、链表、指针、队列、深搜、广搜、最小生成树、最短路、折半查找、冒泡排序、快速排序、选择排序、散列表
• 不要总想着拿满分，学会拿暴力算法分，这要求我们对于每一种潜在的数据结构和算法都有理解
• 会分析自己算法的时间和空间复杂度，一定不能错，结合暴力算法拿分可观
• 学会使用伪代码，知道老师这题考察什么，不关键的地方可以用伪代码表示

王道老师们总结了408算法题可能的考法，后期会发给大家，大家先打好基础和掌握选择题

Week 2 学习计划总览

Week 2 学习计划总览

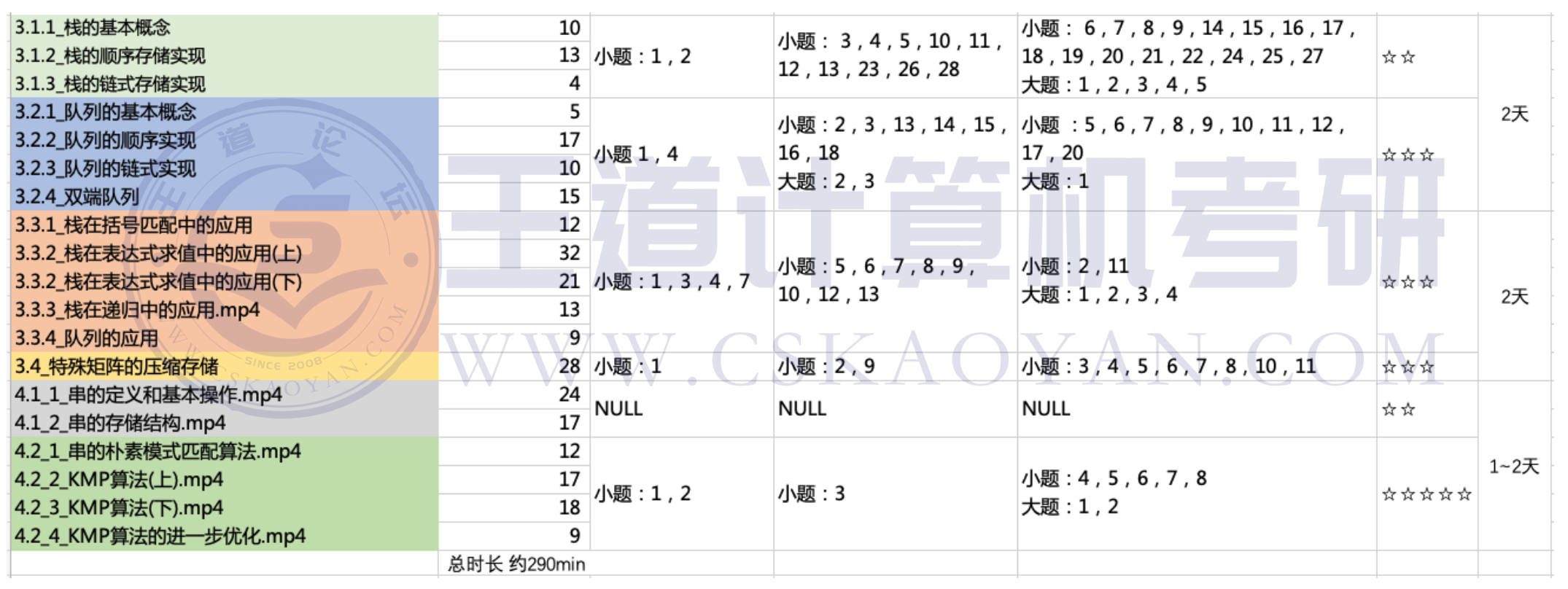
本周复习提要

本周，我们会学习第三、第四章。第三章将学习栈和队列两种数据结构，以及矩阵的压缩存储。第三章是408中出小题的高频章节，偶尔也会出大题。栈和队列本质上是操作受限的线性表，因此只要掌握好第二章的内容，第三章的学习难度就不大。相比之下，第四章的KMP算法是难点，但算不上重点，一般就考察一个小题。如果觉得第四章学起来很困难，请不要悲伤，不要哭泣，几乎所有人都会这么觉得。当然，在第一轮复习中，大家还是应该静下心来搞定这块硬骨头。

Day 8~9 学习计划

3.1 栈

学习建议

• 明确栈是线性表的一种，满足"先进后出”的特点
• 学会模拟栈的操作，408常在小题考察出栈序列的合法性、栈的应用

到目前为止，408尚未考过“栈”的算法题，但这并不意味着今后不会，“栈”其实很适合用来出算法题。就像以前都不考“图”相关的算法题，但是去年突然考了“图”的遍历，让很多同学猝不及防。

因此，在第一轮复习，时间还算充裕时，不应着急赶进度，慢下来练练码算法，会让你在后几轮复习中更有底气。据反馈，往年很多同学在后几轮复习中，由于时间紧张，没有精力练算法题，内心会很慌（算法题是最难在短时间内突破的大题，只能靠平时多积累）。

第一轮复习，质量远比速度更重要！

考研修仙

• 道上人：理解栈的定义及特点

  • 小题 1、2

• 道上佬：掌握栈的基本操作

  • 小题 3-5、10-13、23、26、28

  错题：小题 3

• 道上仙：理解共享栈，掌握链栈，能判断出栈顺序是否正确

  • 小题 6-9、14-22、24、25、27
  • 大题 1
  • 大题 2
  • 大题 3
  • 大题 4
  • 大题 5

  其中，3、4两题的风格和408算法题很类似，值得认真体会。

  错题：小题 9、22、25 / 大题 3（2）【不需要建栈】

  不清晰：大题 5【复用代码的方式】

3.2 队列

学习建议

• 明确队列是线性表的一种，满足“先进先出”的特点
• 学会模拟队列的操作，408常考察双端队列和队列结合、循环队列、队空队满条件
• “循环队列”挺多坑的，会考察判空、判满等很细节的地方

考研修仙

• 道上人：理解队列的定义及特点，比较栈和队列

  • 小题 1、4

• 道上佬：掌握队列的基本操作，掌握链队

  • 小题 2、3、13-16、18
  • 大题 2
  • 大题 3

  如果做了第二章我们推荐的大题，大家会发现，线性表的"逆置"是一个很重要的算法，在408历年真题中，已经考察过两年。而在本节大题2题中，我们又会用队列和栈实现"逆置"。

  错题：小题 14

• 道上仙：掌握循环队列，理解双端队列

  • 小题 5-12、17、20
  • 大题 1

  不清晰：小题 10 / 大题 1

Day 10~11 学习计划

3.3 栈和队列的应用

学习建议

• 学会比较栈与队列
• 408常考察出栈序列、栈和队列的应用

考研修仙

• 道上人：了解栈和队列有哪些应用

  • 小题 1、3、4、7

• 道上佬：理解这些应用

  • 小题 5-10、12、13

• 道上仙：实现这些应用并学会模拟

  • 小题 2、11
  • 大题 1
  • 大题 2
  • 大题 3
  • 大题 4

  不清晰：大题 2、4

  不会做：大题 3

3.4 特殊矩阵的压缩存储

学习建议

• 408常考察压缩后下标计算、适合压缩的矩阵类型

• 注意三元组的顺序（行优先）

  思考：如何快速计算下标

  思考题参考答案：带入两个或三个值

考研修仙

• 道上人：矩阵压缩的原理、优点

  • 小题 1

• 道上佬：各类矩阵如何压缩

  • 小题 2、9

• 道上仙：矩阵压缩的计算与实现

  • 小题 3-8、10、11

  不清晰：小题 4、11

Day 12~13 学习计划

今天和明天，我们将学习第四章——串。

本章的KMP算法是一个难点，根据往年反馈，通常要反复看多次，才能理解该算法。很多往届同学会因学习该算法而摇身变成“暴躁老哥”，达成劝退效果。因此，先给大家打个预防针，KMP算法是公认的难理解，需要反复多次学习，从多个角度理解。

今天大家先按照自己的节奏尝试看王道书理解KMP算法的原理，然后再看视频，之后再回王道书加深理解。KMP算法很复杂，不太可能考察手写代码，大家着重理解算法原理，学会求next数组，并能模拟算法执行的过程即可。

---

不知道昨天大家有木有看王道书研究过KMP算法？很懵逼？那就对了，每个人第一次学KMP都这样。经过昨天的自我折磨，可能对KMP算法能有个不太清晰的认知，今天可以再结合视频课程重新捋一捋，理解next数组的原理，而不是死记算法的过程。

---

是不是看了好久，KMP算法求next数组的代码好像跟你的大脑不适配一样💔

本章KMP是难点但不是重点,出题频率很低，KMP算法很复杂，不太可能考察手写代码，大家着重理解算法原理，学会求next数组，并能模拟算法执行的过程即可!

人总是这样，简单的喜闻乐见，难的眉头紧皱，没关系，攻坚克难路上搭好脚手架，慢慢来，一点一点攻克。

目前有些童鞋可能因为正答率不太高感到有些灰心丧气，其实duck不必，咸鱼老师当年做题的记录——23题错5题，大佬都是这样经历过来的，哈哈，所以第一轮做题建议大家带着查漏补缺的目的，通过做题情况找出自己的薄弱处，进而加强学习补充，这样才能步步为赢~

4.1-2 串的定义和实现 / 串的模式匹配

学习建议

• 在408考研大纲中，“字符串的模式匹配"被归为“查找算法”的一个小分类，有史以来考察过两三次选择题，考察频率并不高。因此即便这个部分学起来有点困难，也不用着急，relax~
• 要能够手写“朴素模式匹配算法”的代码
• “KMP算法”由于较为复杂，因此不太可能考察手写代码，只要能模拟算法执行过程即可。

考研修仙

• 道上人：

  • 小题 1、2

• 道上佬：

  • 小题 3

• 道上仙：

  • 小题 4-8
  • 大题 1
  • 大题 2

  不清晰：小题 1(2)(3)

本周内容总结

过去这一周，我们学习了第三、第四章的内容。其中，栈和队列的应用是小题的考察重点，大家要掌握手算模拟包括“括号匹配”、“表达式求值”等算法的运行过程。大家好好做课后习题，就能体会到这个部分的考察方式，做题才是王道呀。 第三章矩阵的压缩存储部分，说白了是数学问题，只要能理解矩阵压缩的策略，就能自己推出怎么把压缩后的矩阵下标映射为原矩阵的下标。而模式匹配算法，虽然单独作为一章，但考察频率很低，难度吧，又挺让人头大的，不知道大家学懂了没？

Week 3 学习计划总览

Week 3 学习计划总览

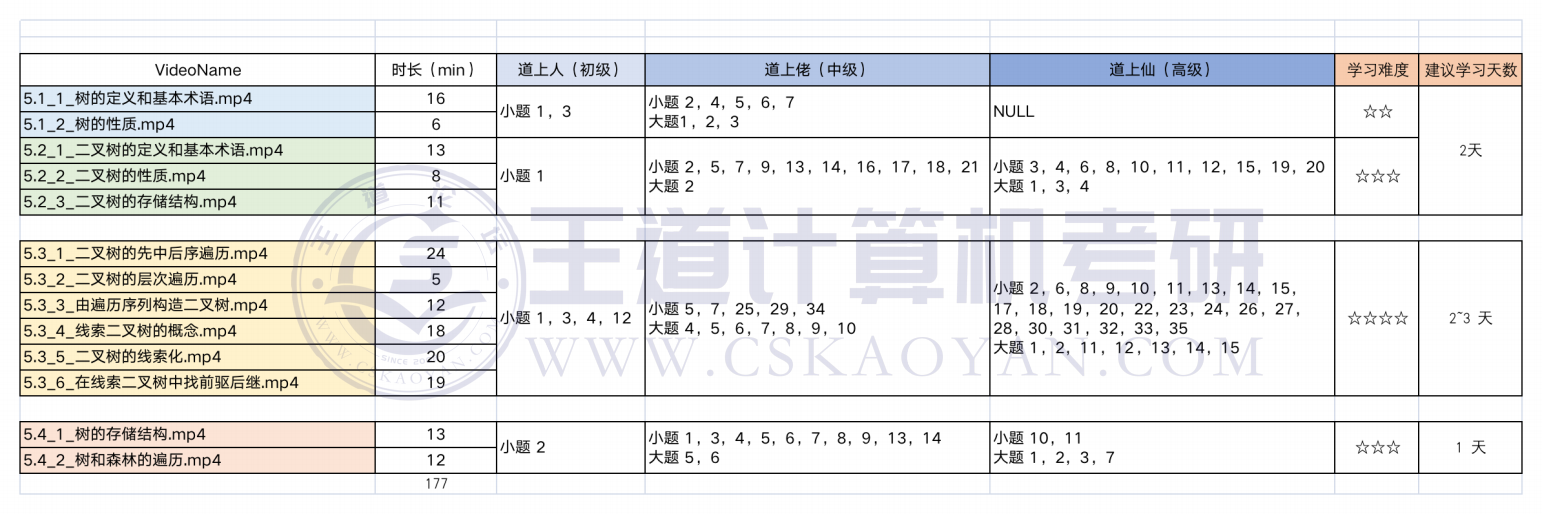
本周复习提要

本周，我们将进入“树和二叉树”的学习，这个部分通常考察小题，也有两年考察了算法题，不过都是基于“二叉树的遍历”的算法。因此在学习本章内容的时候，还是以小题训练为主。对于大题，当前阶段只需掌握二叉树的先、中、后、层序遍历的代码即可。另外，“线索二叉树”也是一个难点，但通常只会在小题中进行考察，打个预防针，挺难学的，做好心理准备。有能力的同学可以提前学5.5小节。

下周，我们将挑一天时间为大家组织线上期中考试，考察范围是前五章。

Day 15~16 学习计划

5.1 树的基本概念

学习建议

• 注意总结树的度、高度、结点数量、叶子结点数量等概念之间的数学关系。每年必考
• 5.1这个小节内容较少，建议5.1+5.2一起，用两天来学习

考研修仙

• 道上人：理解树的概念、特点

  • 小题 1、3

• 道上佬：掌握树的结点、度、高度关系并计算

  • 小题 2、4-7
  • 大题 1
  • 大题 2
  • 大题 3

  易错点：树的高度的定义：是结点的层数

5.2 二叉树的概念

学习建议

• 注意总结二叉树的度、高度、结点数量、叶子结点数量等概念之间的数学关系。每年必考
• 完全二叉树是很特别的存在，非常喜欢考察。另外，第八章我们会学习一种排序算法——堆排序。这种算法就是基于完全二叉树的顺序存储来实现的。因此完全二叉树的顺序存储，也要好好理解哦

考研修仙

• 道上人：理解二叉树的概念、特点

  • 小题 1

• 道上佬：掌握二叉树的顺序存储和链式存储，掌握完全二叉树、满二叉树的高度计算和父子结点编号关系

  • 小题 2、5、7、9、13、14、16-18、21
  • 大题 2

  错题：小题 2（注意要有编号结点一定要存在）

• 道上仙：二叉树（包括完全二叉树、满二叉树）的结点、高度、度的综合计算

  • 小题 3、4、6、8、10-12、15、19、20
  • 大题 1
  • 大题 3
  • 大题 4

  错题：小题 4（注意分析“结点最少”是什么意思），15（计算错误），19（计算错误），20（不会，除特殊值外有别的方法吗？）

  错题：大题 1（注意如何从结点数计算高度），4（不会分析）
  易错点：小题10/11：完全二叉树中有叶结点的不一定是最后一层，也有可能是导数第二层

Day 17~19 学习计划

5.3 二叉树遍历与线索二叉树

学习建议

• 王道书上出现的先序、中序、后序、层次遍历需要重点掌握

• 二叉树每个遍历序列都有其对应的线索二叉树，对于有些结点，计算机在访问的时候很难直接得到在某个遍历序列中的前驱和后继，而通过建立线索二叉树，我们可以很快访问到任何结点在该遍历序列的前驱和后继

• 408中常考察多种遍历顺序结合，以及给出一颗二叉树，求出线索指针所指

  思考：线索二叉树的作用

  思考题参考答案：快速找到结点的前驱和后继

考研修仙

• 道上人：掌握二叉树前中后序遍历，掌握对应递归代码（认识非递归）

  • 小题 1、3、4、12

• 道上佬：掌握二叉树层次遍历

  • 小题 5、7、25、29、34
  • 大题 4
  • 大题 5
  • 大题 6
  • 大题 7
  • 大题 8
  • 大题 9
  • 大题 10

• 道上仙：掌握多种遍历序列构造唯一二叉树、掌握二叉线索树

  • 小题 2、6、8-11
  • 小题 13-15、17-20
  • 小题 22-24、26-28
  • 小题 30-33、35
  • 大题 1
  • 大题 2
  • 大题 11
  • 大题 12
  • 大题 13
  • 大题 14
  • 大题 15

错题记录

模糊：小题 1

一方面，AB是可以互推的，肯定是错的。

另一方面，根据【结点】与【叶子结点】的选项区别，可以构造一个只有左孩子的分支结点来验证ABD选项，都能反驳结论，只有C选项不符合这种情况。

不会：小题 4

后序遍历中，n在m前的三种情况：左右、左根、右根

注意：

• 这里的左、右都是指子树中的任意结点，而不仅仅是直接的孩子结点）

• 题目要求“n在m前的条件是”意味着需要一个充分条件即可（而不必是充要条件），那么只需要从选项分析是否存在有符合选项但是不符合题意的情况。

不会：小题 5

首先，层次遍历不涉及树结点的父子关系，所以不可能是层次遍历。

这里的“找到从m到n的路径”（能逆序给出也行），可以通过后序【非递归】遍历，访问到n结点时，函数中的“工作栈”中就保存着到从n结点到根结点的路径（路径上就有m结点），此时只需要依次弹出“工作栈”，直到碰到m结点，就能生成从n到m的路径。

中序和前序遍历由于“工作栈”保存的并不是严格的父子结点（有可能是兄弟结点），所以程序没有办法得出严格的严格的父子结点路径。

模糊：小题 6

模糊：小题 8

不会：小题 9

模糊：小题 14

模糊：小题 15

不会：小题 23

不会：小题 28

模糊：小题 29

考虑两层结点中的根：

• 先序遍历（找根后继）：根 左 右
  • 左右都存在：根（左根 左左 左右）（右根 右左 右右）
  • 左不存在：根（先序前驱）（右根 右左 右右）
  • 右不存在：根（左根 左左 左右）（先序后驱）
  • 左右都不存在：根（先序前驱）（先序后驱）
• 中序遍历（找根后继）：左 根 右
  • 左右都存在：（左左 左根 左右）根（右左 右根 右右）【右子树往左找到尽头】
  • 左不存在：（中序前驱） 根（右左 右根 右右）【右子树往左找到尽头】
  • 右不存在：（左左 左根 左右）根（中序后驱）
  • 左右都不存在：（中序前驱）根（中序后驱）
• 中序遍历（找根前驱）：左 根 右
  • 左右都存在：（左左 左根 左右）根（右左 右根 右右）【左子树往右找到尽头】
  • 左不存在：（中序前驱） 根（右左 右根 右右）
  • 右不存在：（左左 左根 左右）根（中序后驱）【左子树往右找到尽头】
  • 左右都不存在：（中序前驱）根（中序后驱）
• 后序遍历（找根后继）：左 右 根
  • 后继不在根结点及其后代上，没有办法直接找到

不会：小题 31

不会：小题 34

• 【性质1】前序遍历序列＋中序遍历序列＝唯一的二叉树。

  当前序遍历序列确定时，能得到几种不同的中序遍历序列，就有几种二叉树。

• 由于在非递归实现中，

  • 先序遍历是访问结点并把该结点压入栈（第1次碰到访问）；

  • 中先序遍历是先把结点压入栈，然后等需要出栈时再出栈来访问（第2次碰到时访问）

  • 所以，先序遍历序列与中序遍历序列有存在如下关系：

    【性质2】先序序列对应入栈序列，中序序列对应出栈序列。

• 因此，问题就转化为

  以序列a,b,c,d为入栈次序，则出栈序列的个数为多少？

• 根据栈的性质：

  【性质3】对于n个不同元素进栈，出栈序列的个数为$\frac{1}{n+1}{C}_{2n}^n$。

  • 这里a,b,c,d共4个元素，故n=4，可以计算得到出栈序列的个数为14。

模糊：小题 35

模糊：大题 4

层次遍历的逆序可以辅以栈来实现。

模糊：大题 5

总体思想是改造层序遍历来实现。这主要是由于只有层序遍历才能直接通过目前函数的运行状态获得当前结点的层次信息。先/中/后序遍历由于需要到弹栈来找回之前的祖先节点，导致没有办法在不改造节点（额外记录层次信息）的情况下保存节点的层次信息。

方案1：建立一个层数记录队列

为树结点同步建立一个层数记录队列，与树结点同步出入队，并记录对应结点的层数。

这个方法的空间复杂度稍大。

unsigned countLevel(const tree &root) {
 std::queue<node *> Q;
 std::queue<unsigned> Qt;
 node *ptr = nullptr;
 unsigned count = 0;
 Q.push(root);
 Qt.push(1);
 while (!Q.empty()) {
     ptr = Q.front(), Q.pop();
     count = Qt.front(), Qt.pop();
     if (ptr->lchild) {
         Q.push(ptr->lchild);
         Qt.push(count + 1);
     }
     if (ptr->rchild) {
         Q.push(ptr->rchild);
         Qt.push(count + 1);
     }
 }
 return count;
}

方案2：采用双端队列

利用临时变量last记录本层的最后一个结点。

• 初始情况下last即为根节点（可以理解为根节点就是其所在层的最后一个节点），检测到的层数为1（即根节点这一层已被检测到）。
• 每次从队列中弹出节点时，检查是不是本层的最后一个结点，是的话说明本层的结点已经全部出队，下一层的结点已经全部入队，即可更新临时变量last为下一层的最后一个结点（即此时队列里的最后一个节点），同时将检测到的层数+1。
• 最后返回检测到的层数即可。

unsigned countLevel2(const tree &root) {
 std::queue<node *> Q;
 unsigned count = 0;
 node *ptr = nullptr, *last = root;
 Q.push(root);
 while (!Q.empty()) {
     ptr = Q.front(), Q.pop();
     if (ptr->lchild) {
         Q.push(ptr->lchild);
     }
     if (ptr->rchild) {
         Q.push(ptr->rchild);
     }
     if(ptr == last){
         ++count;
         last = Q.back();
     }
 }
 return count;
}

正常：大题 6

模拟从先序和中序序列中手算恢复二叉树

tree build_from_order(ElemType preOrder[], ElemType inOrder[], size_t N) {
    // 假设 preOrder[0], inOrder[0] 都不放内容，即数组下标从1开始
    // preOrder[], inOrder[] 即题中的A和B
    if (N < 1)
        return nullptr;
    tree root = new node;
    unsigned i;
    root->val = preOrder[1];
    // 寻找根节点在inOrder中的位置
    for (i = 1; i <= N; ++i) {
        if (inOrder[i] == root->val) {
            break;
        }
    }
    root->lchild = build_from_order(preOrder + 1, inOrder, i - 1);
    root->rchild = build_from_order(preOrder + i, inOrder + i, N - i);
    return root;
}

Day 20 学习计划

5.4 树、森林

学习建议

• 这一节重点和常考点是树森林与二叉树的相互转化，记住“左儿子右兄弟”，两者遍历序列的对应关系也需要理解记忆：树先根～二叉树先序、树后根～二叉树中序
• 注意树的子结点是有先后顺序的，儿子不能随意换位置

考研修仙

• 道上人：理解树和森林的存储结构

  • 小题 2

• 道上佬：掌握树、森林与二叉树的转换

  • 小题 1、3-6

  • 小题 7-9、13、14

  • 大题 5

  • 大题 6

• 道上仙：理解树的先根、后根遍历与对应二叉树先、中、后、层次遍历的关系，认识并查集

  • 小题 10、11

  • 大题 1

  • 大题 2

  • 大题 3

  • 大题 7

本周内容总结

过去这一周，我们学习了树、二叉树、森林相关的知识，上周这部分是408小题的命题重点，不过题型的重复率还算比较高。

树和二叉树的度、结点数、高度、叶结点数等参数之间的关系经常作为计算推理题考察，应熟练掌握。

二叉树的遍历部分，需要掌握先序、中序、后序、层序遍历的代码，曾经有两年的算法题就是基于二叉树的遍历算法来考察的。至于“遍历的非递归实现”，本质上和递归实现没有区别，不过是手动实现结点入栈、出栈的过程而已，空间复杂度上也和递归实现是同等数量级。因此，遍历的非递归实现可以解决的问题，递归实现也可以解决，且代码会更加简洁。因此，对于算法题，可重点关注先中后序遍历的递归实现。

依据往年的经验，线索二叉树常在小题中考察，因此在第一轮复习时，可以先不掌握线索二叉树的相关代码，把精力放在小题上，后序几轮复习，根据自身能力，再来尝试突破线索二叉树的相关代码（线索二叉树考察算法题的概率不大）。复习的时间精力有限，把时间精力投入到考试重点可更高效，也更能建立学习自信。

最后，树和森林这个部分，要掌握树、森林 如何转化为 二叉树，同时，要掌握树、森林的性质相关计算（曾经有一年的大题考察过），对代码的考察概率不大。

Week 4 学习计划总览

Week 4 学习计划总览

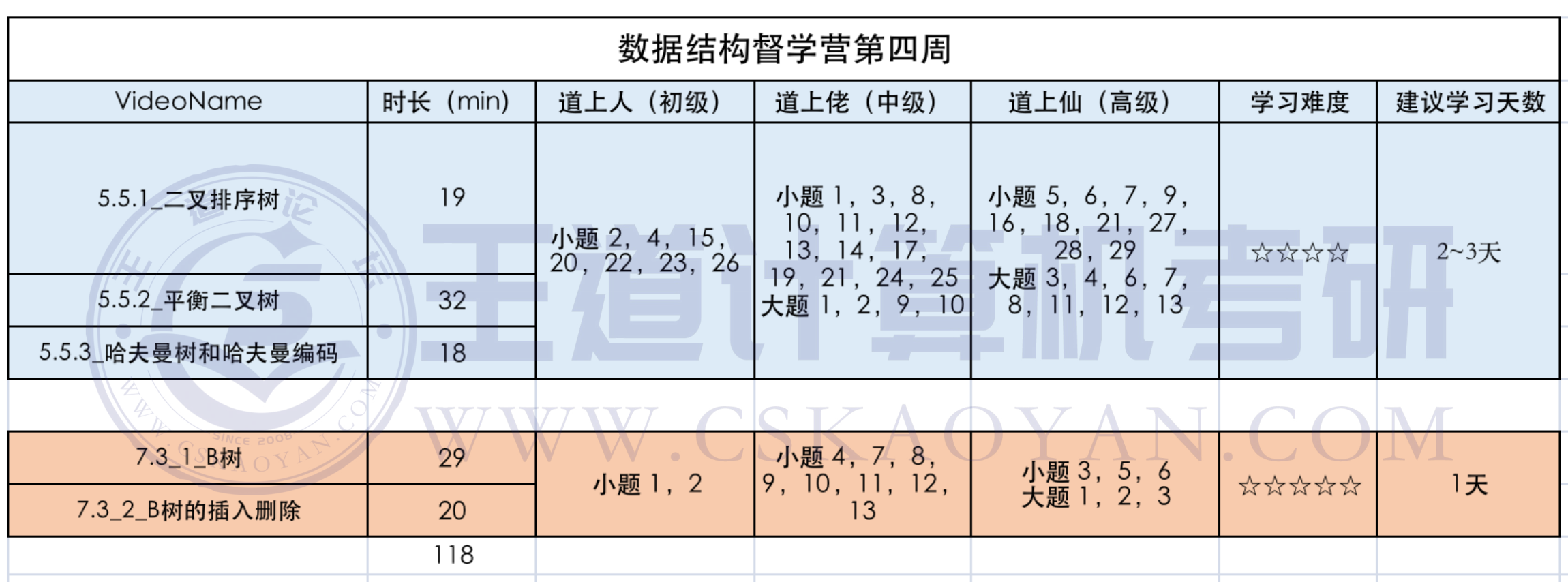
本周复习提要

本周，我们将学习第五章最后一个小节——5.5 树与二叉树的应用，这个小节才是大题的命题重点，需要认真学习。本节中，包含“二叉查找树”和“平衡二叉树”相关知识，这部分知识和第七章的“B树”有较强的联系，因此学完 5.5 后，我们会趁热打铁，提前学习7.3.1，B树相关的内容（B+树先不学，只学B树即可）

5.5+7.3.1 的内容大概需要学习3天左右学习。学完之后，剩余的时间，大家可以试着复习之前已经学过的内容，自己体会“复习”的感觉。

本周五晚上会组织第一次期中考试，详情如下：

• 考试平台：中国大学MOOC，只能用电脑网页版
• 考试题型：单选题+综合应用题
• 考试范围：数据结构专业课督学营前四周学习内容
• 评分方式：单选题由平台自动给分，综合应用题根据参考答案，自助评分。
  注：我们会在后台随机挑选10位同学，由咸鱼老师人工判卷（综合应用题部分）
• 考试时间：周五晚上7点
• 可参加考试的人群：已购买全程班、vip班、定向班、数据结构单科班的所有用户
• 注意：规定时间参加不了在线考试的学员，可以后面做题练习，只是不能提交算分！

Day 22~24 学习计划

5.5 哈夫曼树和哈夫曼编码

二叉排序树 / 平衡二叉树 / 哈夫曼树和哈夫曼编码

学习建议

• 二叉排序树的中序遍历是一个递增序列，平衡二叉树是一种特殊的二叉排序树
• 平衡二叉树的任意一棵子树也是平衡二叉树
• 设高为i的平衡二叉树最少结点数为a[i]，其中a[1]=1，a[2]=2，则递推式为a[i+2]=a[i]+a[i+1]+1
• 哈夫曼树默认是二叉树，且只有度为0和度为2的结点，之后我们还会学习m叉哈夫曼树
• 二叉排序树和哈夫曼树都有可能在大题中出现，他们的定义以及相关代码都要求掌握

考研修仙

• 道上人：掌握二叉排序树、平衡二叉树、哈夫曼树的概念，理解二叉排序树、平衡二叉树、哈夫曼树的特点

  • 小题 2、4、15、20
  • 小题 22、23、26

• 道上佬：掌握二叉排序树、平衡二叉树的插入删除操作，掌握哈夫曼树带权路径长度的计算

  • 小题 1、3、8、10、11
  • 小题 12-14、17
  • 小题 19、21、24、25
  • 大题 1
  • 大题 2
  • 大题 9
  • 大题 10

• 道上仙：掌握二叉排序树、平衡二叉树的综合计算、掌握哈夫曼树的建树

  • 小题 5-7、9
  • 小题 16、18、21
  • 小题 27-29
  • 大题 3
  • 大题 4
  • 大题 6
  • 大题 7
  • 大题 8
  • 大题 11
  • 大题 12
  • 大题 13

Day 25 学习计划

7.3 B树

学习建议

• B树是m叉排序树的变种，每个结点至多有m棵子树，关键字数=子树数-1
• B树根结点（如果不是叶结点）至少有两棵子树，除根外的非叶结点至少有⌈m/2⌉个分支，B树所有叶结点为空
• B树不太可能在大题中考察，选择题中主要考察性质、插入删除操作以及关键字计算

考研修仙

• 道上人：掌握B树的概念

  • 小题 1、2

• 道上佬：掌握B树的高度与结点、关键字的计算

  • 小题 4、7-9

  • 小题 10-13

• 道上仙：理解B树插入、删除的过程，了解B树的应用

  • 小题 3、5、6
  • 大题 1-3

• 本文内容版权归 王道论坛 所有，本人仅出于个人计划目的收集记录。
• 版权声明： 未经 王道论坛 许可，不得以任何方式转载、修改！